معايير الرخصة المهنية للمعلمين والمعلمات الرياضيات للمرحلة الثانوية والمتوسطة 2020 – 1441
معايير الرخصة المهنية لمعلمي الرياضيات معايير الرخصة المهنية لمعلمي الخاصة باختبار الرخصة المهنية للمرحلة للمرحلة الثانوية والمتوسطة،أوضحت هيئة تقويم التعليم ماهية الرخصة المهنية للمعلمين والمعلمات. قالت تقويم التعليم: الرخصة المهنية للمعلمين والمعلمات هي وثيقة صادرة عن الهيئة وفق معايير محددة ، يكون حاملها مؤهلا لممارسة مهنة التدريس وفق مستويات محددة وفترة زمنية محددة ، الرخصة المهنية من شروط الحصول على الدرجة المهنية الصادرة عن وزارة التربية والتعليم، شاهدأيضاً معايير الرخصة المهنية للمعلمين والمعلمات الكيمياء 2020 – 1441 “من هنا“ وأيضاً معايير الرخصة المهنية للمعلمين والمعلمات الرياضيات المرحلة الابتدائية 2020 – 1441 “من هنا“
نبذة عن معايير الرخصة المهنية:
يفرض التغير الاقتصادي والتقني على المؤسسات التربوية الاعتناء بإكساب الطلاب معارف ومهارات تتلاءم مع احتياجات سوق العمل ومتطلبات العصر ،وتسهم في إعدادهم للأدوار الإيجابية الفاعلة في مجتمعاتهم ،وتطلب ذلك التغيير في وظائف المدرسة وفي دور المعلم الذي لم يعد قاصرا على تلقين المعلومات والمعارف لطلابه أو تغطية محتوى المنهج في مدة زمنية محددة ،بل امتد ليشمل مساعدتهم على التعلم ،والقيام بدور فاعل في تهيئة الطلاب للحياة والقيام بأدوارهم الذاتية والأسرية والمجتمعية بما يتطلبه ذلك من معارف واتجاهات ومهارات.
لذا فإنه جرى تطوير المعايير المهنية للمعلمين في المملكة العربية السعودية لرفع جودة أداء المعلمين وتحسين قدراتهم ومهاراتهم، والتأكيد من أنهم يمتلكون الكفاءة المطلوبة
للانضمام لمهنة التعليم، وأداء هذه الأمانة على الوجه المطلوب. وذلك سعياً لضمان جودة التعليم المقدم للطلاب وتحسين تعلمهم، وتعزيز
دور المعلمين ورفع تأهيلهم، ومتابعة مستوى تقدمهم، وتقديم الدعم والتدريب اللازم لهم، وضبط مسارات تقدمهم المهني.
وأدى التطور في وظيفة المدرسة وأدوار المعلم إلى ارتفاع مستوى التأهيل المطلوب من المعلم؛
لذا فقد سعت وزارة التربية والتعليم ممثلة في مشروع الملك عبدالله لتطوير التعليم العام إلى استقطاب اكفأ المتقدمين من خريجي الجامعات للانخراط في مهنة التدريس ،و طورت لهذا الغرض معايير مهنية جديدة لتحديد ما يفترض أن يتمكن منه المعلم المبتدئ ليكون قادرا على تدريس تخصصه في مراحل التعليم العام بكل كفاءة واقتدار.
ما هي الرخصة المهنية:
الرخصة المهنية هي وثيقة تصدرها الهيئة وفق معايير محددة، يكون الحاصل عليها مؤهلًا لمزاولة مهنة التعليم بحسب مستويات محددة ومدة زمنية محددة، وتعد الرخصة المهنية أحد متطلبات الحصول على الرتبة المهنية الصادرة من وزارة التعليم.
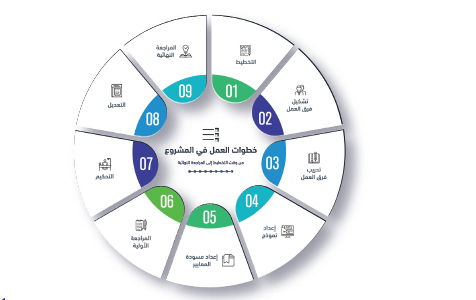
خطوات العمل:
تم العمل في هذا المشروع وفق الخطوات الآتية:
-1التخطيط والإعداد للعمل ،وشمل ذلك ما يلي:
أ .إعداد الإطار العام للمعايير.
ب .إعداد الخطة التنفيذية للمشروع.
ج .إعداد النماذج ،ومواصفات فرق العمل في المشروع.
-2تشكيل فرق العمل ،وتضمن فريق العمل في كل تخصص ما يلي:
أ .مختص علمي في مجال المادة.
ب .مختص تربوي في مجال المادة (مناهج وطرق تدريس المادة).
ج .مشرف تربوي مختص في مجال المادة.
-3تدريب فرق العمل مل ،قتصام المركز بعقد ورشة عمل مكثفة لمدة ثلاثة أيام تضمنت ما يلي:
أ .التعريف بالمشروع ،وأهدافه وخطواته.
ب .التعريف بالمعايير ،واستعراض نماذج من المعايير والتجارب العالمية.
ج .التدريب العملي على صياغة المعايير والمؤشرات.
-4إعداد النموذج الآ ولي ،قتصام الفريق بإعداد نم وذج للعمل للتأكد من ملاءمته للمواصفات والمعايير المطلوبة.
-5 إعداد مسودة المعايير:
بعد إقتصرار النماذج قتصام الفريق بإعداد مسودة المعايير ،واستفاد من التجارب العالمية والعربية المتاحة.
-6الفحص الآولي لمسودة المعايير :قتامت اللجنة المشرفة بالفحص الآولي للمسودة للتأكد من وفائها بالمواصفات والمعايير المطلوبة.
-7التحكيم العلمي :تسلم المسودة وفحصها من اللجنة المشرفة ،أحيلت إلى فريق تحكيم علمي ،يتضمن ثلاثة مختصين علميين وتربويين في مجال المادة لا تقل درجتهم العلمية عن ماجستير.
-8التعديل وفقا لملحوظات المحكمين :بعد انتهاء العمل من التحكيم أعيد مرة أخرى إلى فريق العمل لتعديله وف ًقا لملحوظات المحكمين.
مكونات المعايير: هكذا
تتكون معايير معلمي الرياضيات المستوى الأول من جزأين: الجزء العام الذي يشترك فيه مع جميع معلمي التخصصات الأخرى، والجزء الثاني المتعلق بالتخصص. وتستمل المعايير المشتركة على (10) معايير، تتناولها بالتفصيل (المعايير والمسارات المهنية الوطنية للمعلمين بالمملكة العربية السعودية) فيما تشتمل المعايير التخصصية على (12) معياراً تتناول بنية التخصص وطرق تدريسه، وتصنف هذه المعايير في عدة مجالات. هكذا
المعايير التخصصية: هكذا
تتناول ما ينبغي على معلم الكيمياء معرفته والقدرة على أدائه في التخصص التدريسي وطرق تدريسه،
ويتضمن ذلك المعارف والمهارات المرتبطة بالتخصص، وما يتصل بها من ممارسات تدريسية فاعلة تمل تطبيق طرق التدريس الخاصة، هكذا
والتحلي بالسمات والقيم المتوقعة من المعلم المتخصص بحيث يمثل في ممارساته وسلوكياته الدور المأمول من معلم الكيمياء، هكذا
فيتوقع منه أن يكون متمكن بالحد الأدني من الأداء الفني في التدريس والتعليم، ومتمكن في إطار أوسع من المعرفة الرياضية المتضمنة في مقررات المرحلة المتوسطة والثانوية فهو قادر على تقديم دروس الرياضيات مراعيا عناصر الخطة اليومية وخصائص الطلاب العلقية والنفسية وفق استراتيجيات تدريسية فاعلة ومتنوعة بحيث تراعي طبيعة الموقف التعليمي؛ محققا أهداف تعلم وتعليم الرياضيات المعرفية والمهارية والوجدانية، ومنظما لبيئة التعليم بحيث يظهر بوضوح دور المتعلم في التعليم، ومستعملا تقنيات وأدوات ووسائل معينة في تيسير التعليم، وقادرا على تغيير الأداء التدريسي وتطويره في ضوء معطيات التقويم الشامل للمتعلمين.
إعداد المعايير المهنية: هكذا
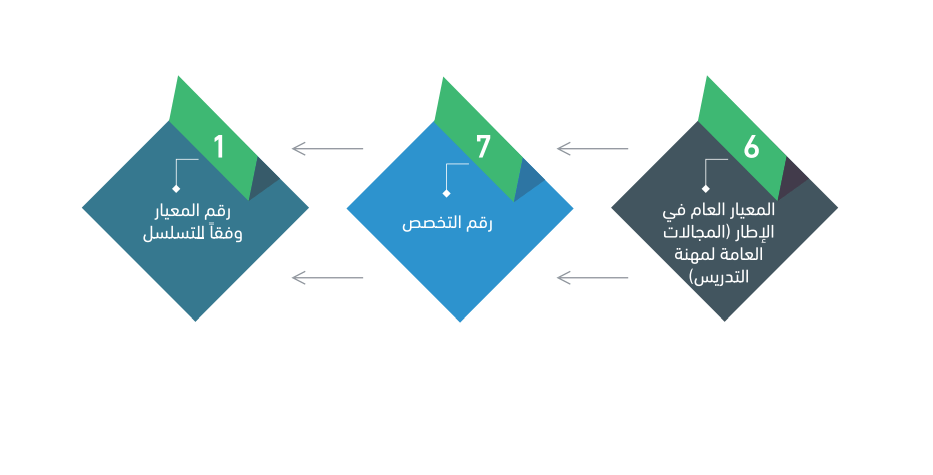
روعي في إعداد المعايير التخصصية أن تكون ضمن الإطار الكلي للمعايير المهنية للمعلم، لذلك رتبت في تسلسل رقمي يبدأ برقم المعيار العام في إطار المعايير العامة، ثم رقم التخصص ثم رقم المعياري التخصص، الذي يفصل في عدد من المؤشرات، كما يتضح من الشكل الآتي:
1. يميز مجموعات الأعداد (الطبيعية، والكلية، والصحيحة، والنسبية، والحقيقية) والعلاقات بينها، وتصنيفاتها المختلفة. هكذا
2 . يجري العمليات (العمليات الأربع، والمقارنة، والجذور والأسس والقيمة المطلقة) على مجموعات الأعداد المختلفة. هكذا
3 . يميز المفاهيم الأساسية لنظرية الأعداد (القاسم المشترك الأكبر، المضاعف هكذا
المشترك الأصغر، قابلية القسمة، الأعداد الأولية وغير الأولية والزوجية والفردية) ويوظفها في حل المسائل.
4 . يوضح مفهوم النسبة والنسبة المئوية والتناسب والمعدل، ويوظفها في حل المسائل. هكذا
5 . يستخدم إستراتيجيات التقدير والحساب الذهني في التحقق من معقولية النتائج وصحتها. هكذا
6 . يحل مسائل رياضية على مجموعات الأعداد المختلفة. هكذا
الإلمام بمبادئ الجبر والدوال الحقيقية: هكذا
1. يصف المفاهيم الأساسية لنظرية المجموعات ويجري العمليات (التقاطع،الاتحاد، الفرق، المتممة) عليها.
2 . يميز العبارات الرياضية (العددية، والجبرية) ويحللها، ويبسطها . هكذا
3 . يحل المعادلات والمتباينات الخطية والتربيعية. هكذا
4 . يحل أنظمة المعادلات الخطية في متغيرين، ويمثلها بيانيًا.
5 . يستكشف الأنماط ويصفها ويكمل العناصر المفقودة فيها، ويعممها. هكذا
6 . يميز بين العلاقات والدوال، ويحدد نوع الدالة ومجالها ومداها. هكذا
7 . يجري العمليات الأربع على الدوال الخطية وكثيرات الحدود من الدرجة الثانية.
8 . يحل مسائل رياضية على مبادئ الجبر والدوال الخطية. هكذا
إتقان المفاهيم الهندسية ونظرياتها:
1. يميز الأشكال ثنائية وثلاثية الأبعاد، ويصفها، ويستنتج خصائصها.
2 . يصف العلاقات الهندسية (تشابه المثلثات، العلاقات بين المستقيمات، والزوايا، ونظرية فيثاغورس)، ويوظفها في حل المسائل.
3 . يعرف معادلة المستقيم في المستوى، ويمثله بيانيًا ويوجد ميله، ويستخدمه في تحديد العلاقة بين المستقيمات.
4 . يوجد المسافة بين نقطتين أو نقطة ومستقيم في المستوى.
5 . . يصف مفهوم الإحداثيات، ويجري التحويات الهندسية (التناظر، الانسحاب،الدوران، التمدد).
6 . يحل مسائل رياضية على المفاهيم الهندسية وتطبيقاتها.
معرفة القياس ووحداته وتطبيقاته:
1. يميز بين وحدات القياس لكل من (الزاوية، الطول، المساحة، الحجم، السعة،الكتلة، درجة الحرارة، الزمن)، ويطبقها، ويجري التحويات بين وحدات القياس
ضمن النظام نفسه.
2 . يجري التحويلات بين وحدات قياس لأنظمة متناظرة.
3 . يوجد محيط ومساحة المثلث والدائرة والأشكال الرباعية والمضلعات المنتظمة.
4 . يوجد حجوم (متوازي المستطيلات، الهرم، المخروط، الأسطوانة)، ويوجد مساحتها الجانبية والكلية. هكذا
5 . يحل مسائل تتضمن مقياس رسم باستخدام النسبة والتناسب. هكذا
6 . يحل مسائل رياضية تطبيقية على القياس. هكذا
الإلمام بمفاهيم الإحصاء والاحتمالات وتطبيقاته: هكذا
1. يجمع البيانات، ويبوبها في جداول، ويمثلها باستخدام (الأعمدة، القطاعات الدائرية، المدرجات التكرارية)، ويحللها ويفسرها.
2 . يجري الدراسات المسحية، ويختار عيناتها، ويستخدمها في التنبؤ. هكذا
3 . يحسب مقاييس النزعة المركزية، والتشتت لمجموعة من البيانات ويحللها ويفسرها. هكذا
4 . يطبق طرق العد الأساسية (قاعدة الجمع، الضرب، التباديل، التوافيق). هكذا
5 . يوظف المفاهيم الأساسية للاحتمالات (فضاء العينة، الحدث، تقاطع واتحاد حدثين، الحوادث المتنافية، الحوادث المستقلة) في إيجاد الاحتمالات.
6 . يحل مسائل رياضية تطبيقية على الإحصاء والاحتمالات. هكذا
معرفة المنطق والاستدلال الرياضي: هكذا
1.يصف التقرير الرياضي، وقيم الصواب، وأدوات الربط، وينشئ جداولها.هكذا
2 . يستخدم الاقتضاء والتكافؤ والقياس المنطقي في حل المسائل. هكذا
3 . يستخدم التبرير الرياضي وطرائق البرهان المختلفة في حل المسائل. هكذا
تطبيق إستراتيجيات تعليم الرياضيات وتعلمها:
1.يوضح مكونات البراعة الرياضية، وكيفية تنميتها لدى المتعلم. هكذا
2 . يصف بنية الرياضيات، ومكونات المعرفة الرياضية بأنواعها، وكيفية تحليلها،وتدريسها، وتقويمها. هكذا
3 . يوظف إستراتيجيات متنوعة في تعليم الرياضيات وتعلمها للوصول لجميع
المتعلمين.
4 . يميز مهارات التفكير الرياضي، وأساليب تنميتها، وتعليمها، وتعلمها.
5 . يصف نظريات التعلم، ويوظفها في تعليم الرياضيات وتعلمها.
6 . يوظف التقنية والأدوات الرياضية واليدويات في تعليم الرياضيات وتعلمها.
حل المسألة الرياضية وتوظيف إستراتيجياتها: هكذا
1.يصف خطوات حل المسألة الرياضية، ويطبقها في حل مسائل حياتية. هكذا
2 . يختار إستراتيجيات مناسبة لحل المسألة الرياضية، ويطبقها، ويقارن بينها. هكذا
3 . يبني مسائل رياضية ويحلها، ويوسع نطاقها هكذا
استخدام التواصل الرياضي وتوظيف مهاراته في تعليم الرياضيات
1 .يستخدم لغة الرياضيات في التعبير عن الأفكار الرياضية بدقة.
2 .يوظــف مهــارات التواصــل الرياضــي بأنواعهــا فــي إيصــال أفــكاره، ومناقشــة أفــكار الآخريــن.
3 .يستخدم أساليب متنوعة في تنمية التواصل الرياضي لدى المتعلمين.
توظيف النمذجة الرياضية وتطبيقات الرياضيات:
شاهد أيضاً:اعلان وزارة الموارد البشرية برنامج الأمن الصحي المنتهي بالتوظيف
1 .يمثل المواقف الحياتية في مسائل رياضية باستخدام النماذج.
2 .يحل المسألة الواردة في النموذج، ويفسره، ويوظفه في تحسين النموذج.
3 .يربط الرياضيات بمجالات التعلم الأخرى، خاصة العلوم الطبيعية والتقنية والهندسة.
4 .يوظف الرياضيات في سياقات الحياة المختلفة
تطبيق الاستدلال الرياضي ومناقشة حجج الآخرين:
شاهد أيضاً:توطين الوظائف التعليمية في منشآت التعليم العام الأهلي
1 .يبني التخمينات والحجج الرياضية، وينقدها، ويقومها.
2 .يبرر النتائج والإجراءات الرياضية الواردة في حل المسائل.
3 .يطبق الاستدلال الاستقرائي والاستنتاجي.
اختبار الرخصة المهنية: هكذا
يعتبر اختبار الرخصة المهنية أحد الأدوات التي تساهم في رفع جودة أداء المعلمين، وتحسين قدراتهم ومهاراتهم، والتأكد من أنهم يمتلكون الكفاءة المطلوبة لأداء مهنة التعليم. وهذا الاختبار يُعد متطلبًا للحصول على الرخصة المهنية للمعلم، ويتكون من جزأين: الجزء الأول: الاختبار التربوي العام ويشترك فيه جميع المعلمين، أما الجزء الثاني فهو اختبار تخصصي يتناول مفاهيم التخصص وبنيته. معايير معلمي الرياضيات الثانوية
رسوم اختبار الرخصة المهنية للمعلمين والمعلمات
شاهد أيضاً: شاهد أول فيديو لحطام صاروخ “لونج مارش 5”
رسوم الرخصة المهنية والاختبار المكون من جزأين (1) العام أو (2) التخصصي، لذا فان تكلفة الرخصة المهنية (300) ريال وفقاً للآتي:
- يلزم 100 ريال لاختبار الرخصة المهنية التربوي العام هكذا
- يتطلب 100 ريال لاختبار الرخصة المهنية التخصصي. هكذا
- 100 ريال لإصدار الرخصة المهنية أو تجديدها أو ترقيتها. معايير معلمي الرياضيات الثانوية هكذا
تكلفة إعادة اختبار الرخصة المهنية: هكذا
- 100 ريال لإعادة اختبار الرخصة المهنية التربوي العام. هكذا
- 100 ريال لإعادة اختبار الرخصة المهنية التخصصي. هكذا
ما هي ضوابط إصدار الرخص المهنية معايير معلمي الرياضيات الثانوية
اُعتُمدت بقرار مجلس إدارة هيئة تقويم التعليم والتدريب في اجتماعه الحادي عشر من الدورة الأولى بتاريخ 14/11/1440هـ الموافق 17/7/2019م، واُعتُمدت التعديلات عليها بقرار من اللجنة التنفيذية لمجلس الإدارة استنادًا إلى تفويض المجلس لها بذلك بتاريخ 8/11/1441 هـ الموافق 29/6/2020م.
ذا
* متابعتكم ¦-
× حسابنا الرسمي بتويتر اضغط هنا
* جديدنا
الخدمة مجاناً لفتره محدوده
لتكن اول من يعلم عن الوظائف الشاغرة ونتائج القبول والتسجيل للوظائف والجامعات
وفرنا لكم تقنية النشر الآلي على التليقرام ليتيح لك الحصول على المستجدات وإعلان نتائج القبول فور صدورها تلقائياً داخل مجموعتك او قروبك على التليقرام، ولتجربة الخدمة مجاناً
انسخ اليوزر الخاص بالروبوت وقم بإضافتة من قائمة اضافة عضو بمجموعتك وتعيينه مشرفاً ليقوم بالنشر التلقائي.
انسخ اليوزر التالي ¦- @Th3eyenbot
× لمناقشة الوظائف مع اقرانك والمهتمين انضم الى مجموعاتنا المخصصة للنقاش عبر التليقرام اضغط هنا
×لمتابعة إعلانات نتائج القبول النهائي
والوظائف الشاغرة عبر قناة عين الخبر اولاََ بأول اضغط هنا
× للإنضمام إلى مجموعات عين الوظائف على الواتس آب اضغط هنا